動物と道具
道具を使う動物
動物番組を見ていると時々「道具を使う動物」が登場します。
ラッコは固い貝を石で打ち付け中身を取り出します。チンパンジーは枝を使い蟻塚の中の蟻を食べます。フサオマキザルは石を使って木の実を割ります。鳥のオウチュウはミーアキャットの警戒のための鳴き声を真似して、ミーアキャットが見つけた餌を横取りします。
今回はこういった道具を使う動物の様子を見ながら考えたいくつかのモデルを記してみようと思います。
道具を使うとはどういうことか?
「道具を使う」とは一体どういうことなのでしょうか?
ラッコの場合、石と貝を組みあわせた結果として、食べることのできる貝の身があります。

この単純なモデルを他にも適用してみます。チンパンジーは枝と蟻塚を組み合わせて蟻を得ます。フサオマキザルは石と木の実を組み合わせ木の実の中身を得ます。オウチュウは擬態した声と「餌を見つけたミーアキャット」を組み合わせて餌を得ます。
最後のオウチュウの例だけが少し違います。この例は自分自身との組み合わせが含まれているからです。モデルを少し変更すると、自分との組み合わせも要素としてあってもよいことがわかります。
修正したモデルだと、ラッコは自身の腕やお腹と石と貝を組み合わせています。チンパンジーやフサオマキザルも同じです。
これは運動を例にすれば当然のことです。スケートボードにうまく乗るためには自身とスケートボードの適合が必要です。
これらのことを「道具」「道具を使う対象」「道具によって生まれた結果」「自分」「環境」という要素にもっともらしく分けてもよいですが、モデルが複雑になる上に、鳴き声のように分離できないものもあります。
また、ラッコは貝をお腹の上に置きますが、フサオマキザルは木の実を地面に置きます。安定させるために組み合わせている何か、という点では役割は同じです。
そこでここでは全てを並列な要素として扱います。

道具を使うことは「何らかの要素が組み合わさり、別の要素になること」とだけにしておくことで、自身は環境なのか?などといった無駄な混乱もなくなります。
使い方の伝達
道具の使い方が伝達される時に見られるのは「真似」です。若いラッコは親が貝を石で割る姿を真似しますし、若いフサオマキザルも群れの中で学びます。結果的に個体の寿命という限界に縛られることなく、同種の家族や群れの中で知が保存されていきます。
同種の中での伝達のほか、種を超えた伝達もあります。
野生から保護されたオランウータンが人間を真似て石鹸やのこぎりを使用するようになる例もあります。さらにそのオランウータンが野生に帰されると、他のオランウータンがそれを真似します。こうして異なる種からも使い方が伝達され定着することもあるのです。
1つ面白い例がチンパンジーです。通常、真似という行為は観察者が観察対象者の様子を一方的に見ながら学びます。しかし、チンパンジーは道具の使い方を知る個体が、使い方を知らない個体をわざわざ呼んで道具を使う様子を見せることがあるそうです。
適合の発見
道具を使うのが上手なチンパンジーもいれば下手なチンパンジーもいます。
では下手なチンパンジーはどのようにしてうまく使えるようになるのでしょうか。私は動物番組を見ながら次のようなモデルを考えました。
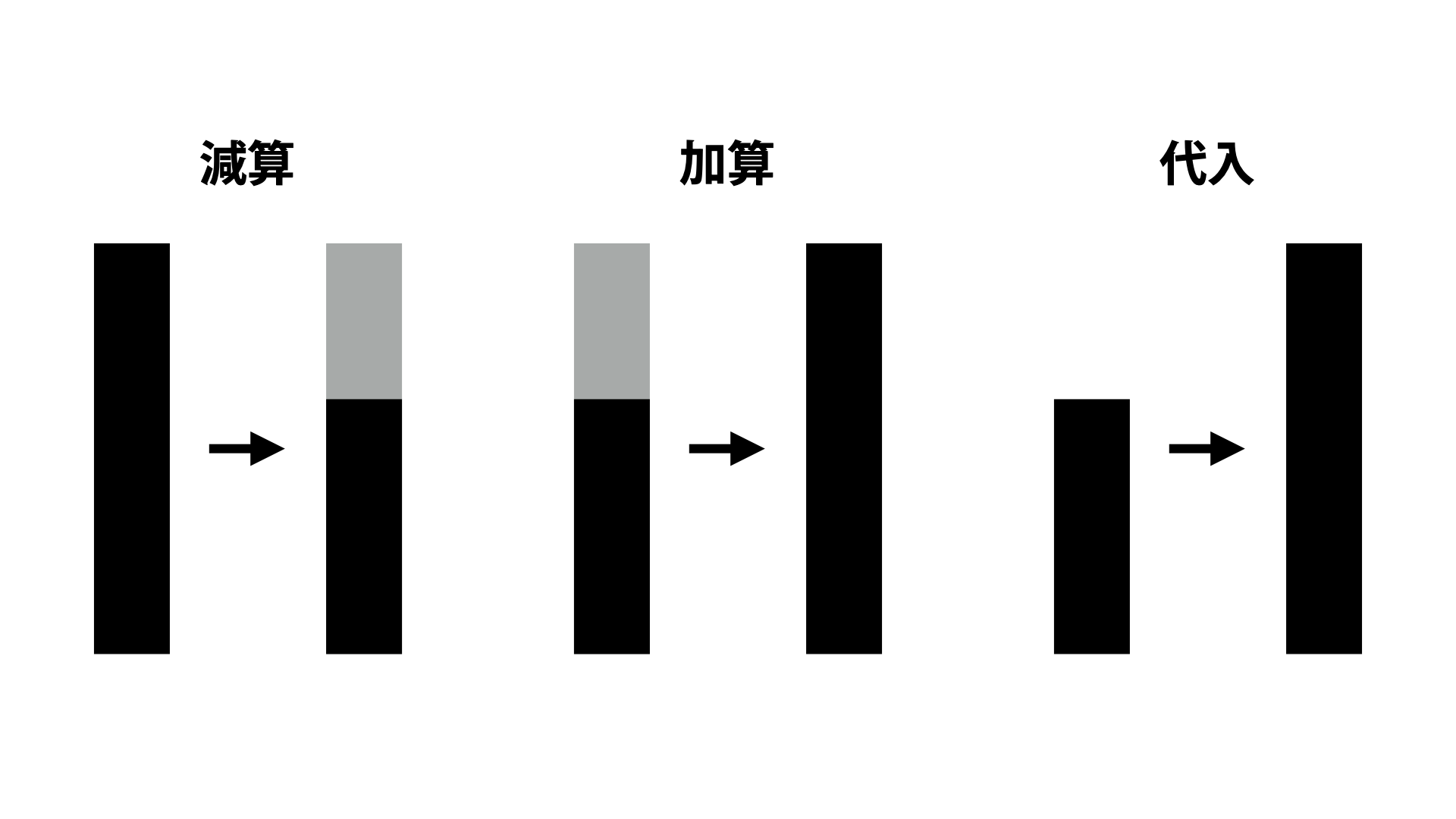
- 減算
- 加算
- 代入
減算
チンパンジーは木の枝を使います。拾った枝についている余計な枝葉をむしりとり調整します。元の形から何かを取り払って別の形にしますので減算型です。
減算型はあるべき形まで減算する行為です。では下手なチンパンジーはどのようにしてあるべき形を見出すのでしょうか?
下手なチンパンジーは下手なりに枝を使います。力ずくで蟻を取ろうとします。もしかするとその過程で枝が偶然折れることもあるのではないかと思いました。なので私は減算といっても「偶然の減算」があるのではないかという仮説を持ちました。
加算
減算があるのであれば加算もあるのではないかと考えました。チンパンジーで言えば短い枝を長くすることはあるのでしょうか。動物番組ではまだそういった例をみたことがありません。
考えてみると枝と枝を組み合わせて1つの長い枝にする行為は複雑です。2つの枝とつなぐ何かが必要で扱う要素が多くなるからです。こういった加算は減算よりも少ないのかもしれません。
一方でサルや鳥は自らの住居を整えます。寝床に適した柔らかさになるまで葉っぱを集めたり、枝を使って産卵に適した巣を作る動物もいます。これらはよく見られる加算型です。
サイチョウという鳥に至っては木の隙間に入って内側から出入り口をくちばしが1つ出る程度まで塞いで卵を産みます。いってみれば道具の中に没入した使い手が道具の形を内側から変化させているので面白い構図です。
加算型もまた「偶然の加算」があるのかもしれません。何かをそこに加えてみたら、もしくは何かが落ちてきたら結果的にいい具合になり、そこからその行為をエスカレートさせるなどです。
寝床や巣作りに限ってみれば自らとの適合度合いでその良し悪しを測れるので、比較的あるべき形の発見は容易なのかもしれません。
代入
下手な個体が上手な個体の使う道具を使うことがあります。自らの道具そのものの改良ではなく別の形を当てはめてみる、というものなので代入型です。よく考えてみるとチンパンジーも枝を一から作るのではなく、身の回りの木の枝を使うので元々代入型ということもできます。
適合点
最後のモデルは適合度合いの視点で考えたものです。減算や加算、代入などによって、時にはこれらを組み合わせながら、道具を使い、ある時点で一定の適合点に達します。
決まった適合点があるわけではなく、見出すものなのだと思いますが、まずは単純なモデルで考えてみました。
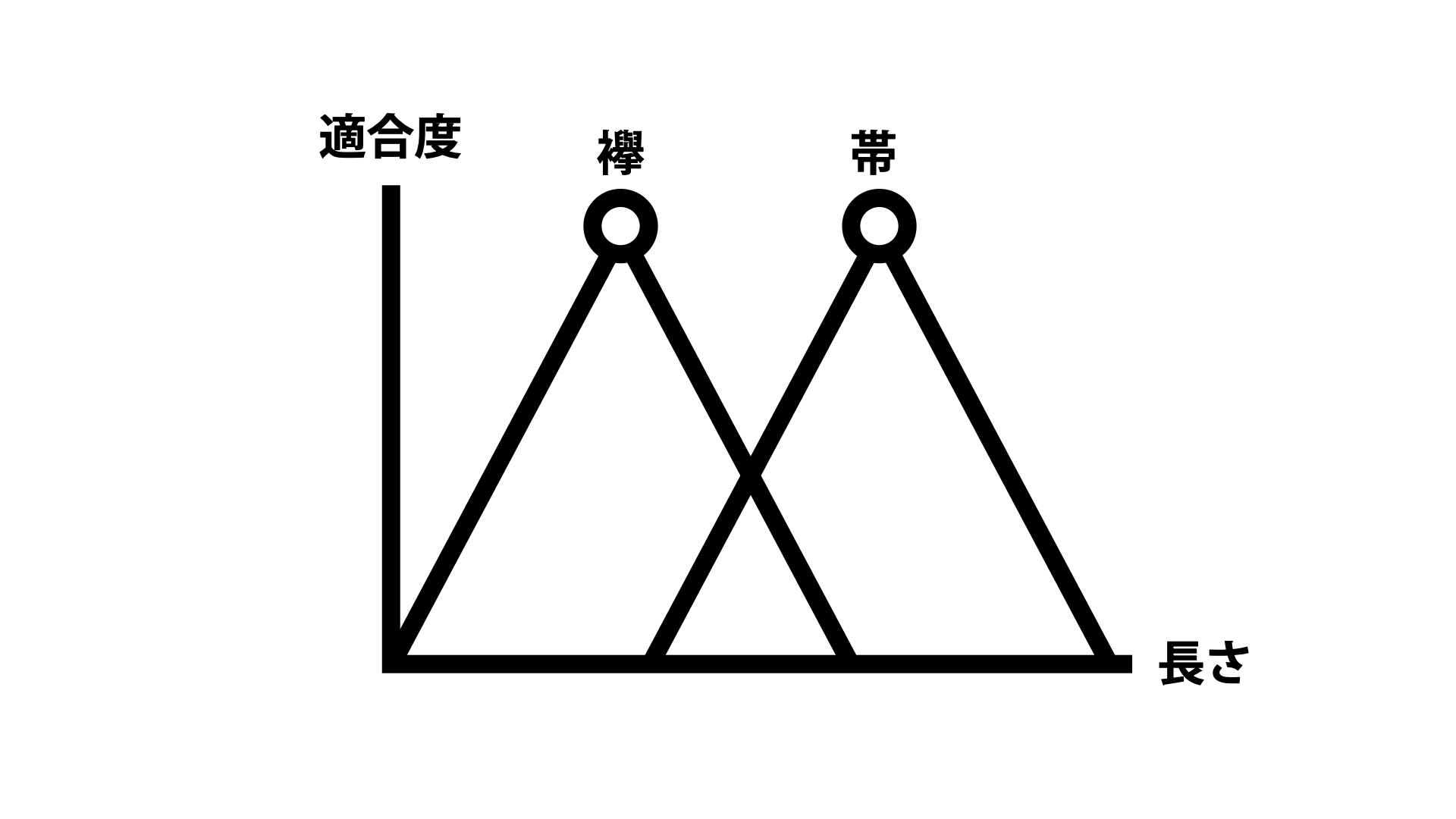
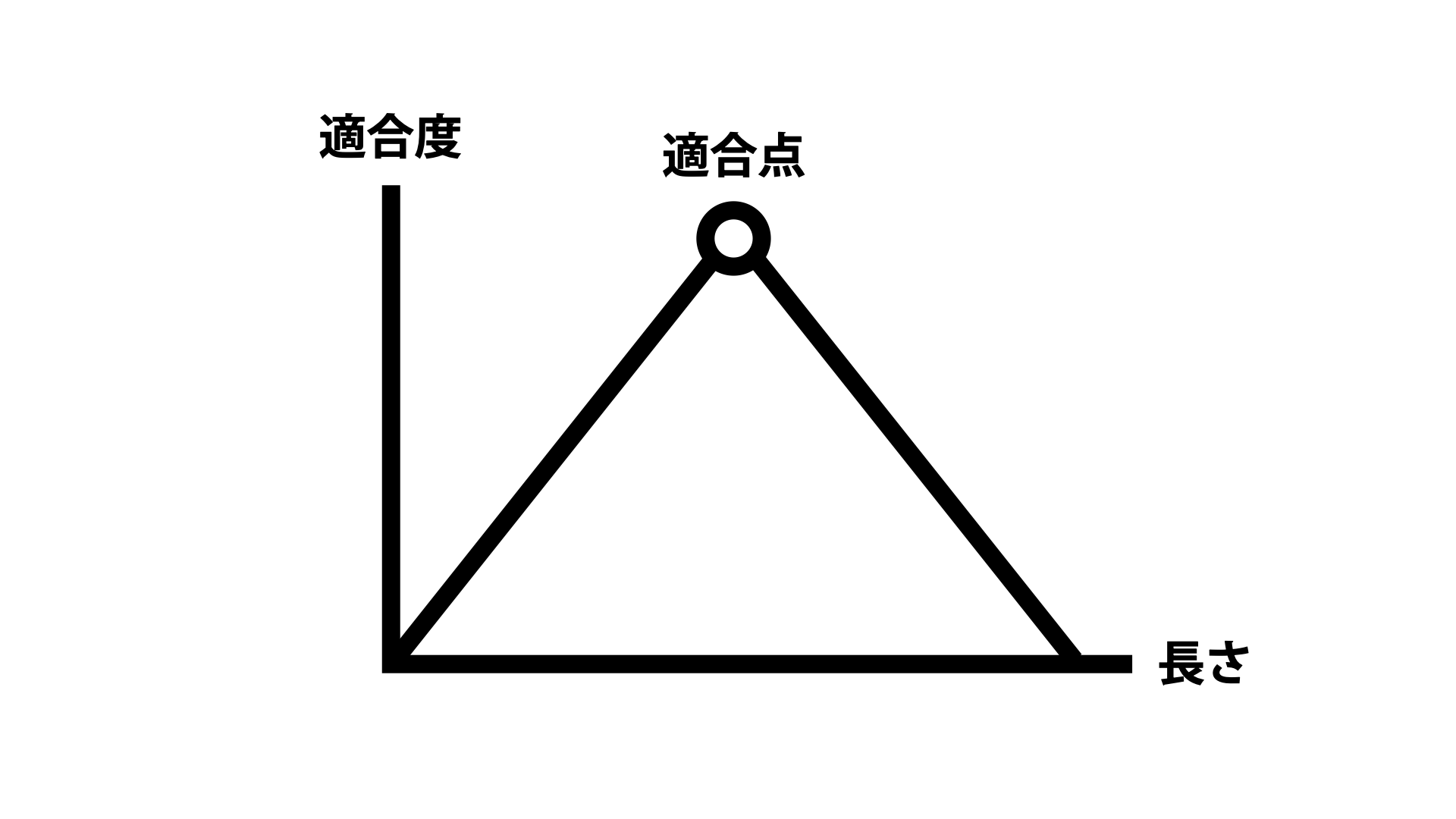
縦軸に適合度合い、横軸に形の度合いがあるとします。例えばチンパンジーであれば枝の長さによって適合度合いが変わります。
枝が長くなるにつれて適合度合が上がりどこかでピークを迎えます。そしてそれ以上に長くなると今度は適合度合が下がっていきます。仮にこのピークを適合点と呼ぶことにしましょう。
1つの道具に対して異なる適合点が求められた場合、トレードオフが発生します。「帯に短し襷に長し」です。帯としての適合点と襷としての適合点が異なる場合、両者の中間の長さだとどちらにしても適合度合が低くなってしまうということです。